









试读已结束,还剩8页未读,您可下载完整版后进行离线阅读
《2017年高考数学知识方法专题10- 数学思想第45练 分类讨论思想》》是由用户上传到老师板报网,本为文库资料,大小为262 KB,总共有18页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 18页
- 262 KB
- VIP模板
- doc
- 数字产品不支持退货
第45练 分类讨论思想[思想方法解读] 分类讨论思想是一种重要的数学思想方法,其基本思路是将一个较复杂的数学问题分解(或分割)成若干个基础性问题,通过对基础性问题的解答来实现解决原问题的思想策略.1.中学数学中可能引起分类讨论的因素:(1)由数学概念而引起的分类讨论:如绝对值的定义、不等式的定义、二次函数的定义、直线的倾斜角等.(2)由数学运算要求而引起的分类讨论:如除法运算中除数不为零,偶次方根为非负数,对数运算中真数与底数的要求,指数运算中底数的要求,不等式中两边同乘以一个正数、负数,三角函数的定义域,等比数列{an}的前n项和公式等.(3)由性质、定理、公式的限制而引起的分类讨论:如函数的单调性、基本不等式等.(4)由图形的不确定性而引起的分类讨论:如二次函数图象、指数函数图象、对数函数图象等.(5)由参数的变化而引起的分类讨论:如某些含有参数的问题,由于参数的取值不同会导致所得的结果不同,或者由于对不同的参数值要运用不同的求解或证明方法等.2.进行分类讨论要遵循的原则是:分类的对象是确定的,标准是统一的,不遗漏、不重复,科学地划分,分清主次,不越级讨论.其中最重要的一条是“不重不漏”.3.解答分类讨论问题时的基本方法和步骤是:首先要确定讨论对象以及所讨论对象的全体的范围;其次确定分类标准,正确进行合理分类,即标准统一、不重不漏、分类互斥(没有重复);再对所分类逐步进行讨论,分级进行,获取阶段性结果;最后进行归纳小结,综合得出结论.体验高考1.(2015·山东)设函数f(x)=则满足f(f(a))=2f(a)的a的取值范围是( )A.B.[0,1]C.D.[1,+∞)答案 C解析 由f(f(a))=2f(a)得,f(a)≥1.当a<1时,有3a-1≥1,∴a≥,∴≤a<1.当a≥1时,有2a≥1,∴a≥0,∴a≥1.综上,a≥,故选C.2.(2015·湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则( )A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当ab时,e1e2答案 D解析 由题意e1==;双曲线C2的实半轴长为a+m,虚半轴长为b+m,离心率e2==.因为-=,且a>0,b>0,m>0,a≠b,所以当a>b时,>0,即>.又>0,>0,所以由不等式的性质依次可得2>2,1+2>1+2,所以>,即e2>e1;同理,当ab时,e1e2.3.(2015·天津)已知椭圆+=1(a>b>0)的左焦点为F(-c,0),离心率为,点M在椭圆上且位于第一象限,直线FM被圆x2+y2=截得的线段的长为c,|FM|=.(1)求直线FM的斜率;(2)求椭圆的方程;(3)设动点P在椭圆上,若直线FP的斜率大于,求直线OP(O为原点)的斜率的取值范围.解 (1)由已知有=,又由a2=b2+c2,可得a2=3c2,b2=2c2.设直线FM的斜率为k(k>0),F(-c,0),则直线FM的方程为y=k(x+c).由已知,有2+2=2,解得k=.(2)由(1)得椭圆方程为+=1,直线FM的方程为y=(x+c),两个方程联立,消去y,整理得3x2+2cx-5c2=0,解得x=-c,或x=c.因为点M在第一象限,可得点M的坐标为.由|FM|==.解得c=1,所以椭圆的方程为+=1.(3)设点P的坐标为(x,y),直线FP的斜率为t,得t=,即y=t(x+1)(x≠-1).与椭圆方程联立,消去y,整理得2x2+3t2(x+1)2=6,又由已知,得t=>,解得-<x<-1或-1<x<0.设直线OP的斜率为m,得m=,即y=mx(x≠0),与椭圆方程联立,整理得m2=-.①当x∈时,有y=t(x+1)<0,因此m>0,于是m=,得m∈.②当x∈(-1,0)时,有y=t(x+1)>0,因此m<0,于是m=-,得m∈.综上,直线OP的斜率的取值范围是∪.高考必会题型题型一 由概念、公式、法则、计算性质引起的分类讨论例1 设集合A={x∈R|x2+4x=0},B={x∈R|x2+2(a+1)x+a2-1=0,a∈R},若B⊆A,求实数a的取值范围.解 ∵A={0,-4},B⊆A,于是可分为以下几种情况.(1)当A=B时,B={0,-4},∴由根与系数的关系,得解得a=1.(2)当BA时,又可分为两种情况.①当B≠∅时,即B={0}或B={-4},当x=0时,有a=±1;当x=-4时,有a=7或a=1.又由Δ=4(a+1)2-4(a2-1)=0,解得a=-1,此时B={0}满足条件;②当B=∅时,Δ=4(a+1)2-4(a2-1)<0,解得a<-1.综合(1)(2)知,所求实数a的取值范围为a≤-1或a=1.点评 对概念、公式、法则的内含及应用条件的准确把握是解题关键,在本题中,B⊆A,包括B=∅和B≠∅两种情况.解答时就应分两种情况讨论,在关于指数、对数的运算中,底数的取值范围是进行讨论时首先要考虑的因素.变式训练1 已知数列{an}的前n项和Sn=pn-1(p是常数),则数列{an}是( )A.等差数列B.等比数列C.等差数列或等比数列D.以上都不对答案 D解析 ∵Sn=pn-1,∴a1=p-1,an=Sn-Sn-1=(p-1)pn-1(n≥2),当p≠1且p≠0时,{an}是等比数列;当p=1时,{an}是等差数列;当p=0时,a1=-1,an=0(n≥2),此时{an}既不是等差数列也不是等比数列.题型二 分类讨论在含参函数中的应用例2 已知函数f(x)=-x2+2ax+1-a在x∈[0,1]上有最大值2,求a的值.解 函数f(x)=-x2+2ax+1-a=-(x-a)2+a2-a+1,对称轴方程为x=a.(1)当a<0时,f(x)max=f(0)=1-a,∴1-a=2,∴a=-1.(2)当0≤a≤1时,f(x)max=f(a)=a2-a+1,∴a2-a+1=2,∴a2-a-1=0,∴a=(舍).(3)当a>1时,f(x)max=f(1)=a,∴a=2.综上可知,a=-1或a=2.点评 本题中函数的定义域是确定的,二次函数的对称轴是不确定的,二次函数的最值问题与对称轴息息相关,因此需要对对称轴进行讨论,分对称轴在区间内和对称轴在区间外,从而确定函数在给定区间上的单调性,即可表示函数的最大值,从而求出a的值.变式训练2 已知函数f(x)=2ex-ax-2(x∈R,a∈R).(1)当a=1时,求曲线y=f(x)在x=1处的切线方程;(2)求x≥0时,若不等式f(x)≥0恒成立,求实数a的取值范围.解 (1)当a=1时,f(x)=2ex-x-2,f′(x)=2ex-1,f′(1)=2e-1,即曲线y=f(x)在x=1处的切线的斜率k=2e-1,又f(1)=2e-3,所以所求的切线方程是y=(2e-1)x-2.(2)易知f′(x)=2ex-a.若a≤0,则f′(x)>0恒成立,f(x)在R上单调递增;若a>0,则当x∈(-∞,ln)时,f′(x)<0,f(x)单调递减,当x∈(ln,+∞)时,f′(x)>0,f(x)单调递增.又f(0)=0,所以若a≤0,则当x∈[0,+∞)时,f(x)≥f(0)=0,符合题意.若a>0,则当ln≤0,即00,即a>2,则当x∈(0,ln)时,f(x)单调递减,f(x)|PF2|,∴=4,=2,∴=2.综上知,=或2.高考题型精练1.若关于x的方程|ax-1|=2a(a>0且a≠1)有两个不等实根,则a的取值范围是( )A.(0,1)∪(1,+∞)B.(0,1)C.(1,+∞)D.答案 D解析 方程|ax-1|=2a(a>0且a≠1)有两个实数根转化为函数y=|ax-1|与y=2a有两个交点.①当01时,如图(2),而y=2a>1不符合要求.综上,00时,要使z=y-ax取得最大值的最优解不唯一,则a=2;当a<0时,要使z=y-ax取得最大值的最优解不唯一,则a=-1.3.抛物线y2=4px(p>0)的焦点为F,P为其上的一点,O为坐标原点,若△OPF为等腰三角形,则这样的点P的个数为( )A.2B.3C.4D.6答案 C解析 当|PO|=|PF|时,点P在线段OF的中垂线上,此时,点P的位置有两个;当|OP|=|OF|时,点P的位置也有两个;对|FO|=|FP|的情形,点P不存在.事实上,F(p,0),若设P(x,y),则|FO|=p,|FP|=,若=p,则有x2-2px+y2=0,又∵y2=4px,∴x2+2px=0,解得x=0或x=-2p,当x=0时,不构成三角形.当x=-2p(p>0)时,与点P在抛物线上矛盾.∴符合要求的点P一共有4个.4.函数f(x)=的值域为________.答案 (-∞,2)解析 当x≥1时,f(x)=logx是单调递减的,此时,函数的值域为(-∞,0];当x<1时,f(x)=2x是单调递增的,此时,函数的值域为(0,2).综上,f(x)的值域是(-∞,2).5.已知集合A={x|1≤x<5},C={x|-a4时,g(a)=f(-2)=7-3a≥0,得a≤,故此时a不存在.(2)当-∈[-2,2],即-4≤a≤4时,g(a)=f=3-a-≥0,得-6≤a≤2,又-4≤a≤4,故-4≤a≤2.(3)当->2,即a<-4时,g(a)=f(2)=7+a≥0,得a≥-7,又a<-4,故-7≤a<-4,综上得-7≤a≤2.7.已知ax2-(a+1)x+1<0,求不等式的解集.解 若a=0,原不等式等价于-x+1<0,解得x>1.若a<0,原不等式等价于(x-)(x-1)>0,解得x<或x>1.若a>0,原不等式等价于(x-)(x-1)<0.①当a=1时,=1,(x-)(x-1)<0无解;②当a>1时,<1,解(x-)(x-1)<0得1,解(x-)(x-1)<0得11};当a=0时,解集为{x|x>1};当01时,解集为{x|Sn-≥S2-=-=-.综上,对于n∈N*,总有-≤Sn-≤.所以数列{Tn}最大项的值为,最小项的值为-.9.已知函数f(x)=,其中a为常数,a≤2.(1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;(2)是否存在实数a,使f(x)的极大值为2?若存在,求出a的值;若不存在,说明理由.解 (1)a=1,f(x)=,∴f(0)=1,∵f′(x)===-,∴f′(0)=0,则曲线在(0,f(0))处的切线方程为y=1.(2)f′(x)==-x[],f′(x)=0的根为0,2-a,∵a≤2,∴2-a≥0,当a=2时,f′(x)=≤0,∴f(x)在(-∞,+∞)内递减,无极值;当a<2时,2-a>0,f(x)在(-∞,0),(2-a,+∞)内递减,在(0,2-a)内递增;∴f(2-a)=(4-a)ea-2为f(x)的极大值,令u(a)=(4-a)ea-2(a<2),u′(a)=(3-a)ea-2>0,∴u(a)在a∈(-∞,2)上递增,∴u(a)0),当a≤0时,f′(x)<0,∴f(x)的减区间为(0,+∞);当a>0时,由f′(x)>0得0a,∴f(x)递增区间为(0,a),递减区间为(a,+∞).(2)由(1)知:当a≤0时,f(x)在(0,+∞)上为减函数,而f(1)=0,∴f(x)≤0在区间x∈(0,+∞)上不可能恒成立;当a>0时,f(x)在(0,a)上递增,在(a,+∞)上递减,f(x)max=f(a)=alna-a+1,令g(a)=alna-a+1,依题意有g(a)≤0,而g′(a)=lna,且a>0,∴g(a)在(0,1)上递减,在(1,+∞)上递增,∴g(a)min=g(1)=0,故a=1.










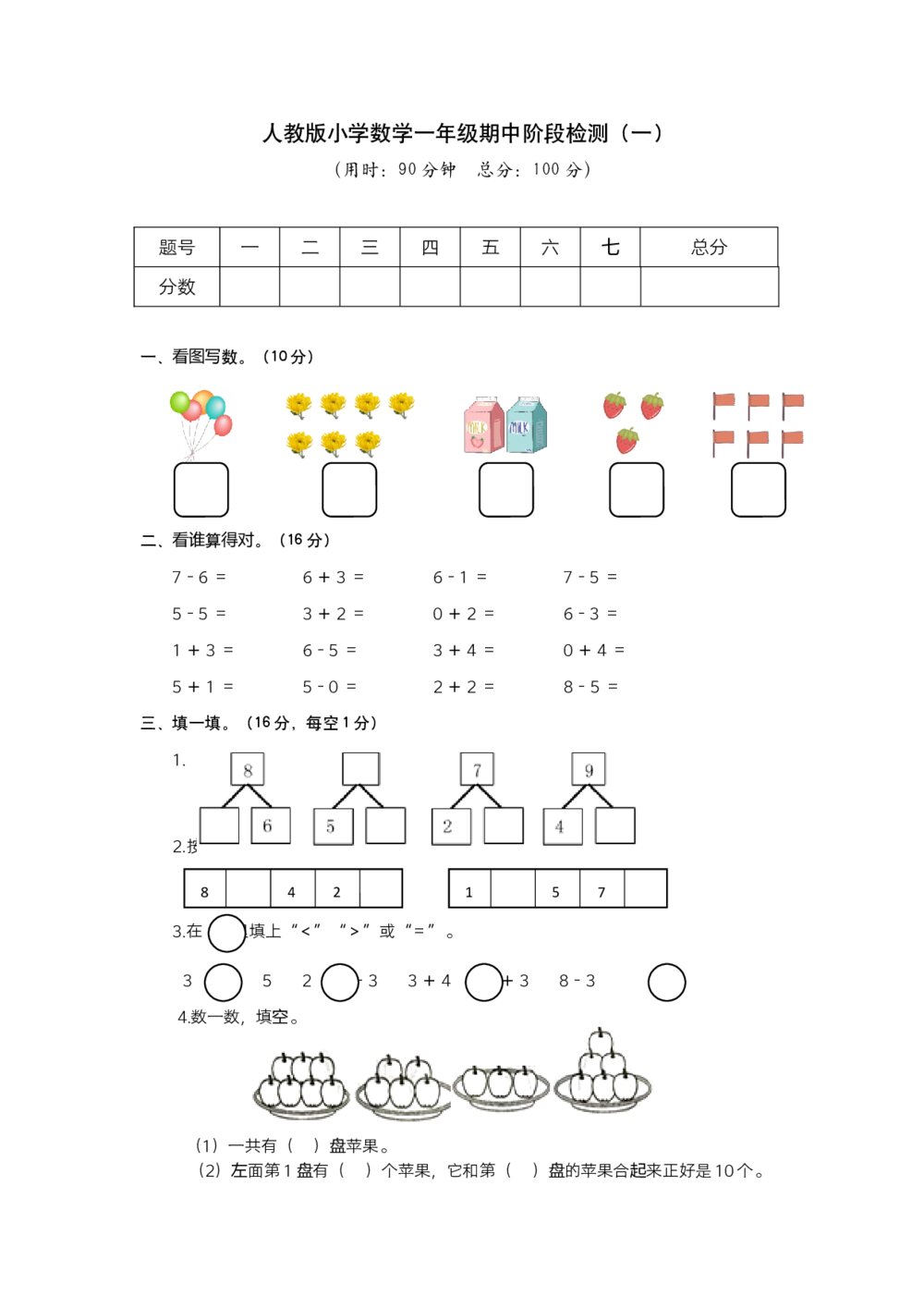 人教版小学数学一年级期中阶段检测(一)试题试卷+参考答案(word版)
人教版小学数学一年级期中阶段检测(一)试题试卷+参考答案(word版) 2011年高考一轮课时训练(理)13.10变量间的相关关系+参考答案 (通用版)
2011年高考一轮课时训练(理)13.10变量间的相关关系+参考答案 (通用版) 2017年高考理科数学三轮冲刺热点题型 中档大题规范练3 数列
2017年高考理科数学三轮冲刺热点题型 中档大题规范练3 数列 2015年海南省高考文科数学试卷word版+答案
2015年海南省高考文科数学试卷word版+答案 六年级数学毕业试卷+答案解析(word版)
六年级数学毕业试卷+答案解析(word版) 2014年天津高考文科数学试题试卷word版+(参考含答案)
2014年天津高考文科数学试题试卷word版+(参考含答案)